Bias, Variance, and In Between
In a given Machine Learning Model, when it’s generating its outputs there will be given sets of tendencies that require attention. Two items that will likely require attention are Bias and Variance.
For a more complete version of the information in this article check here:
Bias
When training a machine learning model, bias describes how closely the model's predictions match the true underlying relationship within the data. Models with high bias tend to make overly simplistic assumptions, resulting in predictions that fail to capture the complexity of real-world data.
Oddly enough I feel that humans do this same thing, but in a more abstract, less mathematical way.
Machine learning bias generally stems from problems introduced by the individuals who design and train the machine learning systems. These people could either create algorithms that reflect unintended cognitive biases or real-life prejudices. Or they could introduce biases because they use incomplete, faulty or prejudicial data sets to train and validate the machine learning systems.
An underfit, high-bias model, performs well on its training set since its basic assumptions apply reasonably well there. However, the model does not glean deeper insights from the training data that would enable accurate predictions on new datasets. As a result, an underfit model generalizes poorly to new, unseen data.
So any Bias that the implementors or even creators of specific algorithms that ML systems are using are capable of carrying human bias when evaluating datasets. ML systems do no naturally seek objective truth, they pass data through their network of nodes and the outputs are only as good as the data they were trained on, and the people tuning the model based on that data.
Variance
When doing target practice, the bullseye of the target is what the shooter is aiming at. If a shooter takes 10 shots at the target, the diameter of the group of shots, and the space in between them as an average would be the closest thing I can think of to describe Variance.
The Inevitable Pick One; Not Both
Due to the nature of real-world data and algorithms and models in the present age, creating models that can perfectly capture a scenario and handle any input data while producing a perfect output, is not yet feasible in most scenarios. Thus, the implementor of the models must make a tradeoff between bias error and variance error.
The total error in a machine learning model can be decomposed into three components: bias squared, variance, and irreducible error. The goal in training a model is to strike the right balance between minimizing bias and variance, thereby minimizing the overall prediction error
So to have a more generalized, more stable prediction with a single model, the way is to play a balance between the error modes. There are other means of accomplishing this work, such as Ensemble Learning.
Conclusion
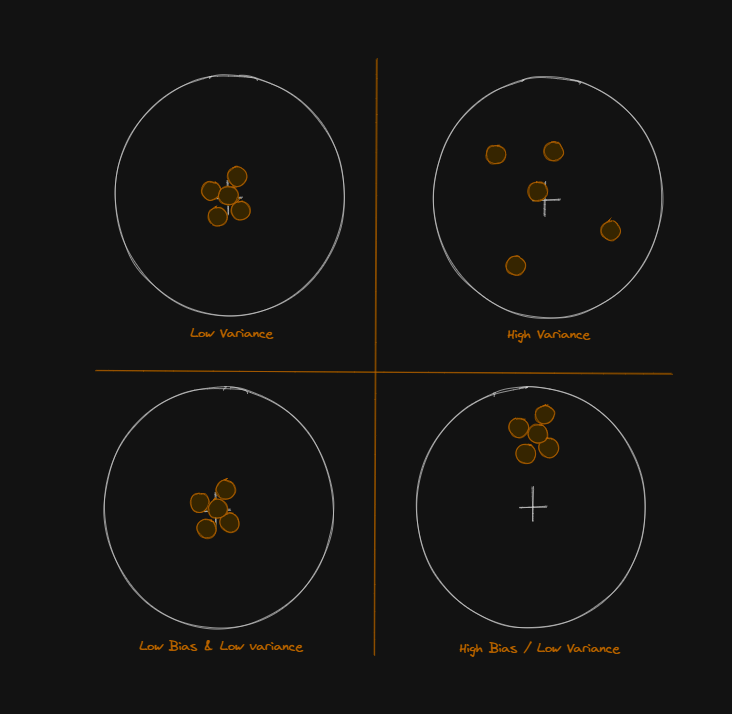
Bias and variance describe error across the same set of dimensions, but also describe two separate error phenomena that will cause less accurate predictions. Bias describes ‘distance from center’ if a set of predictions are grouped on a target graph. Variance describes the ‘distance from other predictions’ if a set of predictions are grouped on the same target graph.
The Bias and variance Trade-off describes either sacrificing Bias for less Variance, or sacrificing some Variance for less Bias in the predictions of the model.